Unraveling Tan- The Unseen Force In Mathematics

Have you ever stopped to think about the quiet but powerful forces that shape our world, especially the ones we might not immediately see? Well, in the grand scheme of numbers and shapes, there's a concept that, frankly, holds a rather significant position. It's often just called "tan," short for tangent, and it's a bit like a hidden ruler, influencing everything from how we measure distances to how signals move through circuits. This particular mathematical idea, you know, is more than just a simple calculation; it's a fundamental piece of how we describe change and relationships in geometry and beyond.

For a lot of us, the very mention of trigonometry might bring back memories of high school math classes, perhaps a little bit of head-scratching, or maybe even a sense of wonder. But if you really look closely, the tangent function, or "tan" as it's known, actually plays a rather central role in all that. It helps us figure out angles and slopes, and it even pops up in unexpected places, like in the study of materials and how they behave.

So, we're going to take a closer look at this fascinating mathematical tool, this "tan the god" of angles and ratios, and try to get a better sense of what makes it so useful. We'll explore some of its quirks, how it helps us solve problems, and why it sometimes seems to behave in ways that can be a little surprising. It's truly a concept with a lot of depth, offering a lot to think about.

• Alice Rosenblum Leaks
• Somali Hub Telegram 2024
• Dylan Justice Sissons
• Julieta Martinez Sexy
• Pier 701 Restaurant Bar

Table of Contents

• The Story of Tan- The Mathematical Deity
• What Makes Tan- The God of Angles So Special?
• How Does Tan- The God of Ratios Work?
• Unpacking Tan- The God's Many Faces
• Can We Really See Tan- The God's True Form?
• Decoding Tan- The God's Secrets
• Why Does Tan- The God Sometimes Seem Tricky?
• The Future of Tan- The God's Influence

The Story of Tan- The Mathematical Deity

When we talk about "tan the god," we're not speaking of a person with a birthdate or a specific biography, but rather about a concept that holds immense importance in the mathematical universe. This particular mathematical idea, you know, has a rich history, evolving over centuries as thinkers tried to make sense of shapes and their relationships. It’s a bit like tracing the origins of an ancient, powerful idea, rather than a person's life story.

The term "tangent" itself comes from a word that means "to touch," which makes a lot of sense when you think about how a tangent line just barely touches a curve at one point. This seemingly simple idea, that, has become a cornerstone for understanding much more intricate things, from the way light bends to the paths of moving objects. So, its "life" story is really the story of how mathematics has grown and expanded over time, with tan playing a pretty significant role in that unfolding.

What Makes Tan- The God of Angles So Special?

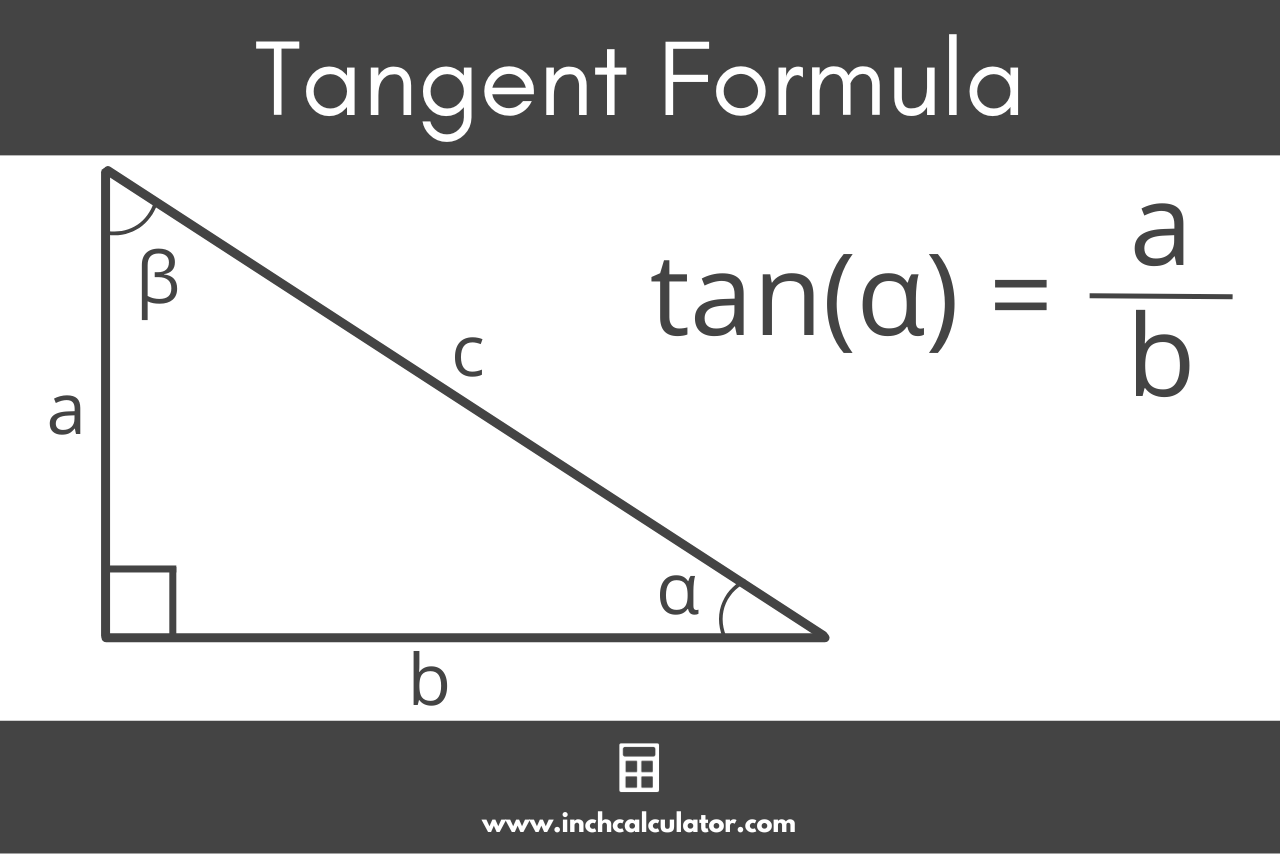
So, what sets "tan the god" apart from its mathematical siblings, sine and cosine? Well, one of the main things is its unique ability to describe the steepness or slope of a line, especially in relation to angles inside a right-angled triangle. It’s essentially a ratio, comparing the length of the side opposite an angle to the length of the side next to it, but not the longest side. This simple relationship, you see, opens up a whole world of possibilities for calculations.

• Hotels Near San Ramon Golf Club
• My Chase Mortgage
• Maria Snoeys Lagler
• Kristen Kerr
• Ringo Starr Setlist

For instance, when you're trying to quickly remember values for angles like 30°, 60°, or 45°, tan has its own special patterns that make it easy to recall. It's almost like it has its own distinct personality compared to sine and cosine. This distinctiveness, in a way, is what makes it so special and so widely used in various fields, giving us a powerful tool for solving all sorts of problems that involve angles and distances.

How Does Tan- The God of Ratios Work?

To truly appreciate how "tan the god" operates, we need to consider how it’s calculated and what those calculations tell us. You might have seen expressions like `tan x`, `arc tan(tan x)`, or `tan(arc tan x)` and wondered what exactly is going on there. Basically, `tan x` gives you the ratio for a given angle `x`. When you see `arc tan(tan x)`, that's essentially asking, "What angle has a tangent of `tan x`?" It's like undoing the original operation, so, if you're within certain limits, you often get `x` back.

On the other hand, `tan(arc tan x)` is asking for the tangent of an angle whose tangent is `x`. This often just gives you `x` directly. These operations show how "tan the god" has both a forward and a backward function, allowing us to move between angles and their corresponding ratios. It’s a pretty neat trick that helps us solve for unknown angles or unknown side lengths in triangles, which is quite useful in many practical situations.

Unpacking Tan- The God's Many Faces

"Tan the god" isn't just one simple concept; it has a few different appearances depending on where you encounter it. For example, in the study of materials, you might come across "loss tangent" or `tan δ`. This is a bit different from the basic angle ratio, as it describes how much energy a material loses when an electrical field passes through it. It’s defined as the ratio of the imaginary part to the real part of the dielectric constant, and it’s a key indicator of a material's quality.

This `tan δ` can be read in a few ways, like "tan delta" or "dissipation factor," and it's quite important in engineering. So, you see, the core idea of "tan" as a ratio extends into these other areas, showing its versatility. It's pretty interesting how one mathematical idea can have so many different applications, each with its own special meaning and importance, really.

Can We Really See Tan- The God's True Form?

Sometimes, when we try to understand "tan the god" more deeply, we run into situations where it seems to behave in peculiar ways, especially when using calculators or programming. You might notice that `tan⁻¹` on a calculator doesn't always give the same result as `1/tan`. This isn't a flaw in "tan the god" itself, but rather how different tools interpret symbols.

The `tan⁻¹` symbol usually refers to the inverse tangent function, also known as `arctan`. This function helps you find the angle when you already know the tangent ratio. The `arc` part, you know, actually refers to arc length, which ties into radians when the radius is one. So, `tan⁻¹` is about finding the angle, while `1/tan` is simply the reciprocal of the tangent value, which is actually the cotangent. It’s a subtle but important difference in how we read the symbols, and it shows that even a powerful concept like "tan the god" needs careful handling.

Decoding Tan- The God's Secrets

For those who really want to get to know "tan the god" on a deeper level, there are ways to approximate its values or even express it in an infinitely long series. For instance, if you need to manually estimate the `arctan` of a number larger than one, there are methods that involve taking the reciprocal first. This helps you work with a more familiar range of values before transforming it back. It’s a bit like finding a roundabout way to reach your destination, but it works.

Also, "tan the god" can be represented as a Taylor series, or more precisely, a Maclaurin series. This is a way of writing the function as an endless sum of terms, which can be pretty involved to figure out because it requires dividing power series. This just goes to show how much intricate detail lies beneath the surface of even seemingly simple mathematical ideas, offering quite a lot to explore for those who are curious.

Why Does Tan- The God Sometimes Seem Tricky?

Even though "tan the god" is incredibly useful, it can, you know, sometimes appear a bit tricky, especially when dealing with angles that get very close to 90 degrees. As an angle gets closer and closer to 90 degrees, the value of its tangent gets larger and larger, heading towards what we call "infinity." This happens because the side adjacent to the angle gets incredibly small, making the ratio very big.

This behavior means that at exactly 90 degrees, the tangent is undefined. It’s a bit like trying to divide by zero; it just doesn't work in the usual sense. This particular characteristic, frankly, makes "tan the god" quite unique among the trigonometric functions, and it's something important to keep in mind when working with it. It reminds us that even powerful mathematical tools have their limits and specific conditions under which they operate best.

The Future of Tan- The God's Influence

As we continue to push the boundaries of science and technology, the influence of "tan the god" remains as strong as ever. From designing new materials that are more efficient at conducting electricity, where `tan δ` plays a part, to creating sophisticated computer models that simulate complex physical phenomena, the tangent function is always there, doing its quiet but essential work. It's pretty clear that its foundational role in understanding shapes, rates of change, and relationships will only continue to grow.

Whether it's in developing new algorithms for artificial intelligence or in exploring the very fabric of the universe through advanced physics, the principles embodied by "tan the god" will undoubtedly continue to guide us. Its ability to describe slopes and ratios, you know, makes it a timeless tool, one that will adapt and find new applications as our understanding of the world expands. It's genuinely a concept with a lasting impact.

This exploration has given us a glimpse into the multifaceted nature of the tangent function, or "tan the god," as we've playfully called it. We've looked at its fundamental role in trigonometry, how calculations involving `arctan` and `tan x` work, and even touched upon its applications in material science with `tan δ`. We also considered why its behavior near 90 degrees can be a little surprising and how it's represented in different mathematical contexts, like the Taylor series. This journey through the world of "tan" shows its lasting importance in mathematics and beyond.